页面

分类

取法其上，得乎其中

《数据结构与算法》学习笔记与一些代码题目的实现

前述

由于最近即将参加某考试，其一科目为数据结构，特此学习以及复习数据结构相关知识并做好笔记。

此博文所涉及图片来自于数据结构与算法不挂科-5小时学完数据结构与算法 课程课件以及王道考研408计算机领学班中的配图。

算法概述

算法一般具备五种特性，分别为：有穷性、确定性、可行性、输入、输出。而我们对算法的好坏评估在于：正确、可读、健壮、高效。

其中我们最主要的是围绕着算法的高效性进行讨论，我们一般以时间复杂度来进行判定。

时间复杂度

时间复杂度，即一个算法在考虑其最坏的场景下需要执行的次数。

for (int i = 0; i < n; i++)
{
    for (int j = 0; j < n; j++)
    {
        printf("%d\n",j);
    }
}

如上述代码，在嵌套for中的printf总共被执行了n^2，我们一般使用O(n^2)来进行表示。

很显然，如果只执行一次，那么就是O(1)。

此处预留时间复杂度相关题目

线性表

线性表是一种一对一的逻辑结构，主要分为两种形式：顺序存储、链式存储。

主要研讨它的特点与基本功能的实现方法(查找、插入、删除、合并)。

顺序存储

其中顺序存储的线性表是采用数组来进行实现的，因此它的相邻元素在内存地址上也是相邻的，并且其具备随机存取的特点，其实就算数组的特点。在Java中的实现就是ArrayList。

定义

struct SqList{
    int data[20];
    int size = 0;
};

基本方法

int insert(SqList *sq, int index, int val)
{
    if (sq == NULL || index > sq->size - 1)
        return 0;
    for (int i = sq->size - 1; i > index - 2; i--)
    {
        sq->data[i + 1] = sq->data[i];
    }
    sq->data[index - 1] = val;
    sq->size++;
    return 1;
}

int del(SqList *sq, int index)
{
    if (sq == NULL || index > sq->size - 1)
        return 0;
    for (int i = index - 1; i < sq->size - 1; i++)
    {
        sq->data[i] = sq->data[i + 1];
    }
    sq->size--;
}

合并有序表

int merge(SqList *a, SqList *b, SqList *c)
{

    int i = 0, j = 0, k = 0;

    while (i < a->size && j < b->size)
    {
        if (a->data[i] < b->data[j])
        {
            c->data[k++] = a->data[i++];
        }
        else
        {
            c->data[k++] = b->data[j++];
        }
    }

    if (i < a->size)
    {
        while (i < a->size)
            c->data[k++] = a->data[i++];
    }
    else
    {
        while (j < b->size)
            c->data[k++] = b->data[j++];
    }
    c->size = a->size + b->size;
}

链式存储

链式存储主要依靠链表进行实现，因此它的元素随机放置在内存的任意位置，而在元素中划分出两个结构，其一为数据，其二为指针域。指针域存放着后一个元素的指针，即它的后驱。而链式存储在Java里的实现就是LinkdList。

定义

struct LinkdNode
{
    int val;
    LinkdNode *node;
};

初始化

LinkdNode *initNode()
{
    LinkdNode *parentNode = (LinkdNode *)malloc(sizeof(LinkdNode));
    LinkdNode *tempNode = parentNode;
    parentNode->val = 0;
    parentNode->node = tempNode;
    for (int i = 1; i <= 5; i++)
    {
        LinkdNode *n = (LinkdNode *)malloc(sizeof(LinkdNode));
        n->val = i;
        n->node = NULL;
        tempNode->node = n;
        tempNode = n;
    }
    return parentNode;
}

基本操作

void display(LinkdNode *node)
{
    if (node->node == NULL)
    {
        printf("\n");
        return;
    }
    printf("%d,", node->val);
    display(node->node);
}

void insert(LinkdNode *node, int index, int val)
{
    LinkdNode *targetParentNode = node;
    for (int i = 0; i < index - 1; i++)
    {
        targetParentNode = targetParentNode->node;
    }

    LinkdNode *newNode = (LinkdNode *)malloc(sizeof(LinkdNode));
    newNode->val = val;
    newNode->node = targetParentNode->node; 
    targetParentNode->node = newNode;
}

void del(LinkdNode *node, int index)
{
    LinkdNode *targetParentNode = node;
    for (int i = 1; i < index - 1; i++)
    {
        targetParentNode = targetParentNode->node;
    }
    targetParentNode->node = targetParentNode->node->node;
}

合并有序表

int merge(LinkdNode *a, LinkdNode *b)
{
    LinkdNode *resultNode = a;
    LinkdNode *tempNode = resultNode;
    a = a->node;
    b = b->node;
    while (a->node != NULL && b->node != NULL)
    {
        if (a->val < b->val)
        {
            tempNode->node = a;
            tempNode = a;
            a = a->node;
        }
        if (a->val > b->val)
        {
            tempNode->node = b;
            tempNode = b;
            b = b->node;
        }
        if (a->val == b->val)
        {
            tempNode->node = a;
            tempNode = a;
            a = a->node;
            b = b->node;
        }

        if (a->node == NULL)
            tempNode->node = b;
        else
            tempNode->node = a;
    }
    display(resultNode);
}

栈和队列

栈与队列本质上是一种受到限制的线性表，其特点体现于栈是一种只允许先进后出的线性表，而队列是一种先进先出的线性表。而在这个部分主要围绕在栈的实现当队列遇到假溢出情况下，循环队列的实现。

栈的实现

定义

struct Stack
{
    int data[20];
    int size = 0;
};

基本操作

int push(Stack *stack,int value){
    if(stack == NULL || stack->size >= 20){
        return 0;
    }
    stack->data[stack->size] = value;
    stack->size++;
    return 1;
}

int pop(Stack *stack){
    if(stack == NULL || stack->size == 0){
        return 0;
    }
    stack->size--; // 无需实际删除元素，下一次push会替换掉。
}

循环队列的实现

对于这部分而言，不考代码，因此只需要记住以下规则。

循环对列的容量: MAX - size - 1
取对内元素数量: ( b - f + m ) % m
判定为满: back + 1 == front
判定为空: back == front

树和二叉树

树主要作为一个一对多的数据结构。

定义

struct BinaryTree
{
    int data;
    BinaryTree *left = NULL;
    BinaryTree *right = NULL;
};

基本概念

子树: 以某个孩子为根的一棵树
叶子节点: 没有孩子的节点
森林: 多棵树
满二叉树: 除了叶子节点，每个节点均有左右两个孩子
完全二叉树: 只是完整但不满，只有最下一层的最右边允许有空缺
深度: 最深的叶子节点所在层数

基本性质

n = 二叉树的结点总数

  1. n = n0 + n1 + n2
  2. 因为 n = 总度数 + 1, 所以 n = n1 + 2n2 + 1
  3. 联合 性质1 与 性质2 可得出， n0 = n2 + 1

第i层的结点最多有 2^(i-1) 个结点
高度为h的二叉树最多有 2^(h-1) 个结点
高度为m的m叉树最多有 (m^(h-1)) / (m - 1) 个结点
完全二叉树的高度 h = log2(n+1) or log2(n) + 1
对于完全二叉树而言，仅需得知结点数就可以推出n0、n1、n2

二叉树的遍历

二叉树的遍历一般分为四种:

  • 先序遍历：当前树 -> 左树 -> 右树
  • 中序遍历：左树 -> 当前树 -> 右树
  • 后序遍历：左树 -> 右树 -> 当前树
  • 逐层遍历

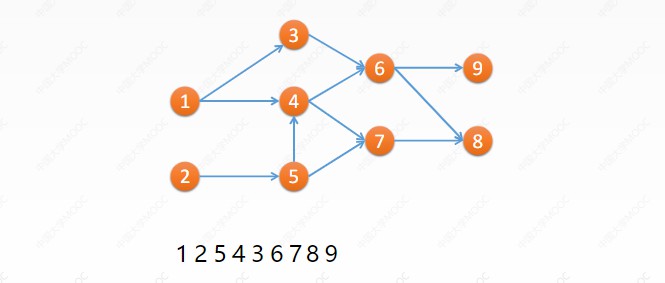
值得注意的是，我们可以依靠中序+先序(后序)遍历的结果来还原出原先的二叉树，因为根据中序的特性我们可以判断出它的左右子树分别是什么。

而在代码之中，顺序的先后之分无非是输出函数prinf和两个递归函数的先后顺序。

void preorder(BinaryTree *bt)
{
    if (bt == NULL)
    {
        return;
    }
    printf("%d ", bt->data);
    if (bt->left != NULL)
    {
        preorder(bt->left);
    }
    if (bt->right != NULL)
    {
        preorder(bt->right);
    }
}

线索二叉树

二叉树如果以链表展示的话，那么将会有n+1个指针域是空的，那么我们可以利用这些空的指针域 “埋入线索” ，即将当前结点的前驱与后继放到里面。

一般的，如果左孩子为空，那么就要把它的前驱结点放进去，反之，右孩子为空则放后继结点。 且在原有的二叉树数据结构上需要增加两个标志位（ltag, rtag）, 如果是0，假如ltag为0，则表左孩子的指针域存放的是左孩子的指针域，反之则是前驱结点。右结点相同。

求二叉树的深度

一个简单的递归。当前深度 = 左右最大深度 + 1。

 int depth(BinaryTree *bt)
{
    if (bt == NULL)
    {
        return 0;
    }
    int leftD = depth(bt->left);
    int rightD = depth(bt->right);
    
    return leftD > rightD ? leftD + 1 : rightD + 1;
}

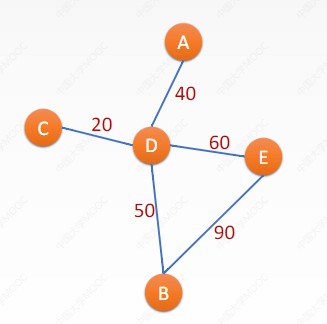
哈夫曼树

特点

  • 越靠近根节点，那么它的权重值就越大，如果我们根据某元素的使用频率来确定权重值，那么也就意味着经常使用的元素在二叉树中占的位置就越靠前，那么获取它的速度也就更快。
  • 如果给这种树中结点的左方向设为0，右设为1，那么每一个节点都拥有了一个唯一的路径，且权重值越高的节点路径越短，一定程度减少存储空间。如上图中权重为8的C节点的路径(编码)便是001.

构造方法

在一组数字(权重)中首先取出两个最小的节点，并将其和设置为它们的父节点。

森林转二叉树

图

图主要作为一个多对多的数据结构。

基本概念

度: 连接的边
有向图: 只允许从A元素到B元素，但不允许B元素到A元素。对于它们度带有限制
无向图: 元素有联系，且度不带有限制，可以任意连接
加权图: 对元素的度进行添加权重，可能是在地图上对于两点的耗时时间为权重，亦可能是对两个任务的花费为权重

图的存储方式

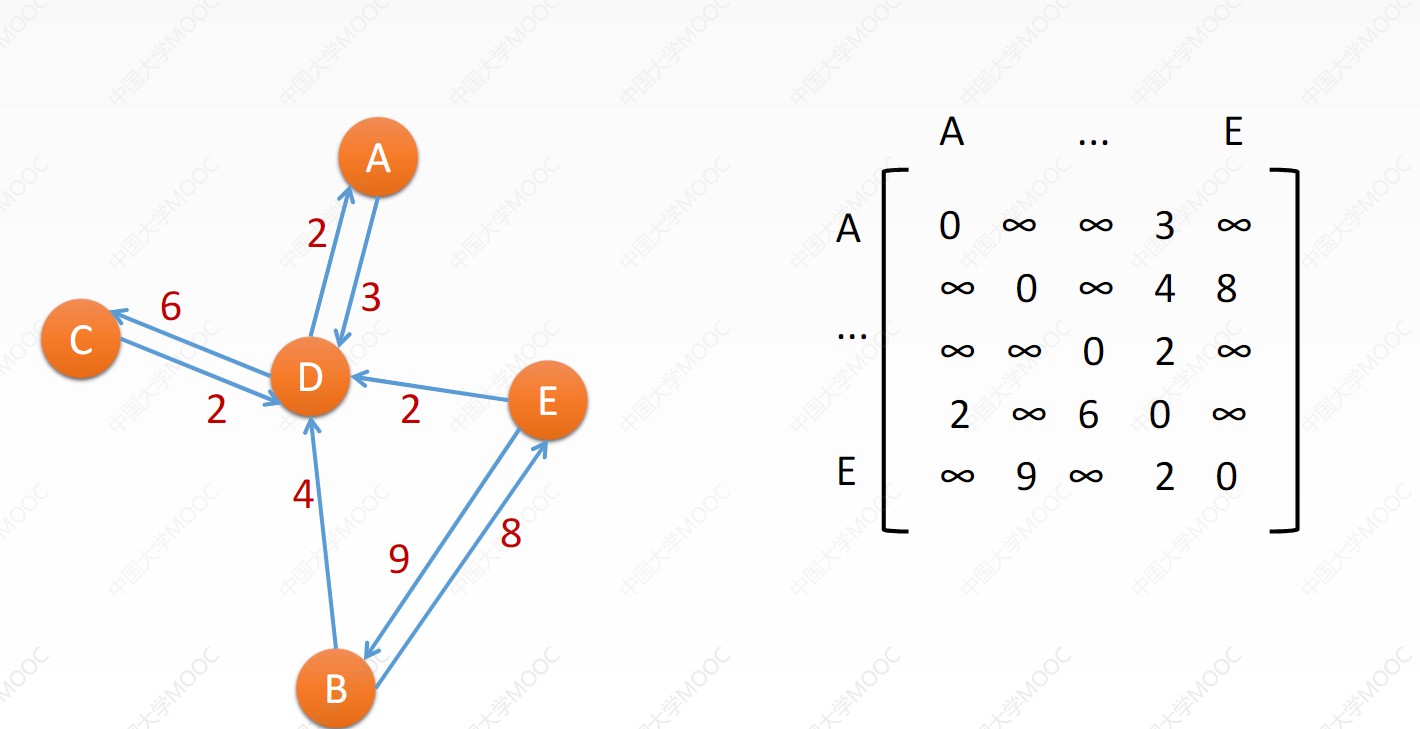
邻接矩阵

图的元素与元素的关系以一个二数组表来进行表示，为0代表是与自己的关系，为∞代表无关系，其他常数代表权重值。
邻接矩阵无论如何都要创建一个二维数组n，但它在搜寻自己与其他元素之间关系的时候借着数组随机访问的特性是O（1）的。因此，邻接矩阵比较适合于稠密矩阵(即元素关系很多的图)。

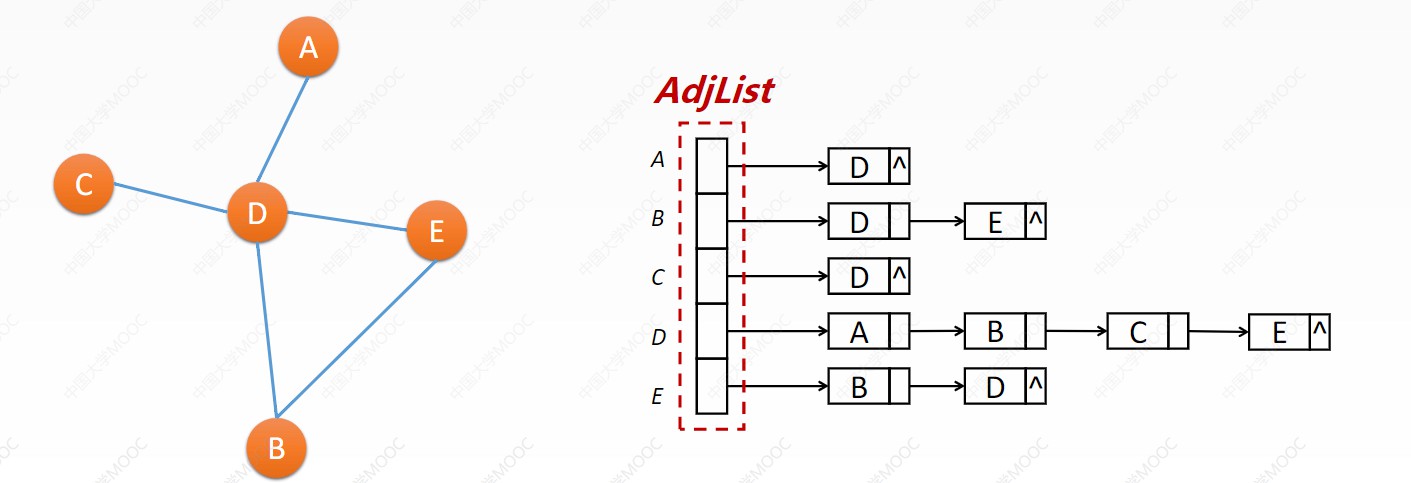
邻接表

使用一个数组链表来存储和某个元素相连接的元素。
优点在于在边比较少的情况下会节省很多的空间，因此，邻接表适合于稀疏图(即元素关系较少的图),缺点是无法直接获取某条边的信息，需要逐步遍历关系链表。

生成树

保证图的连通性的情况下只保留n-1个边，剔除其他边，在保证无环状连接线的情况下它便是一棵树。

最小生成树

在生成树的基础上保证权值相加为最低。

Prim算法(加点法)

选择一个初始节点开始，然后在它的连接中找到一个权重最低的线路(当初始节点已经连接了其他节点时，也可以选择已连接节点的线路)，重复n-1遍。

这种方法使用的便是贪心思想，保证了局部最优。

克鲁斯卡尔


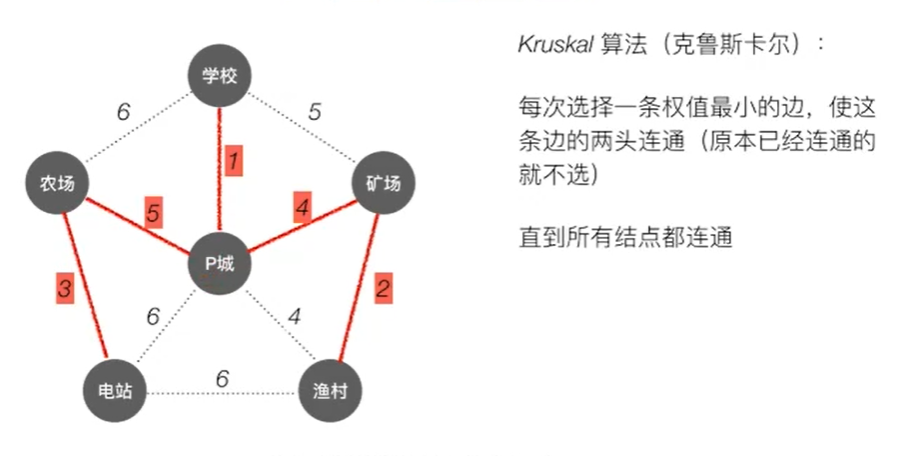
将全局的所有线路遍历出来，以代价进行排序。从最小代价的线路进行连接（两个结点如果已经是联通状态那么就不使用这条线路）。

最短路径（最小代价）

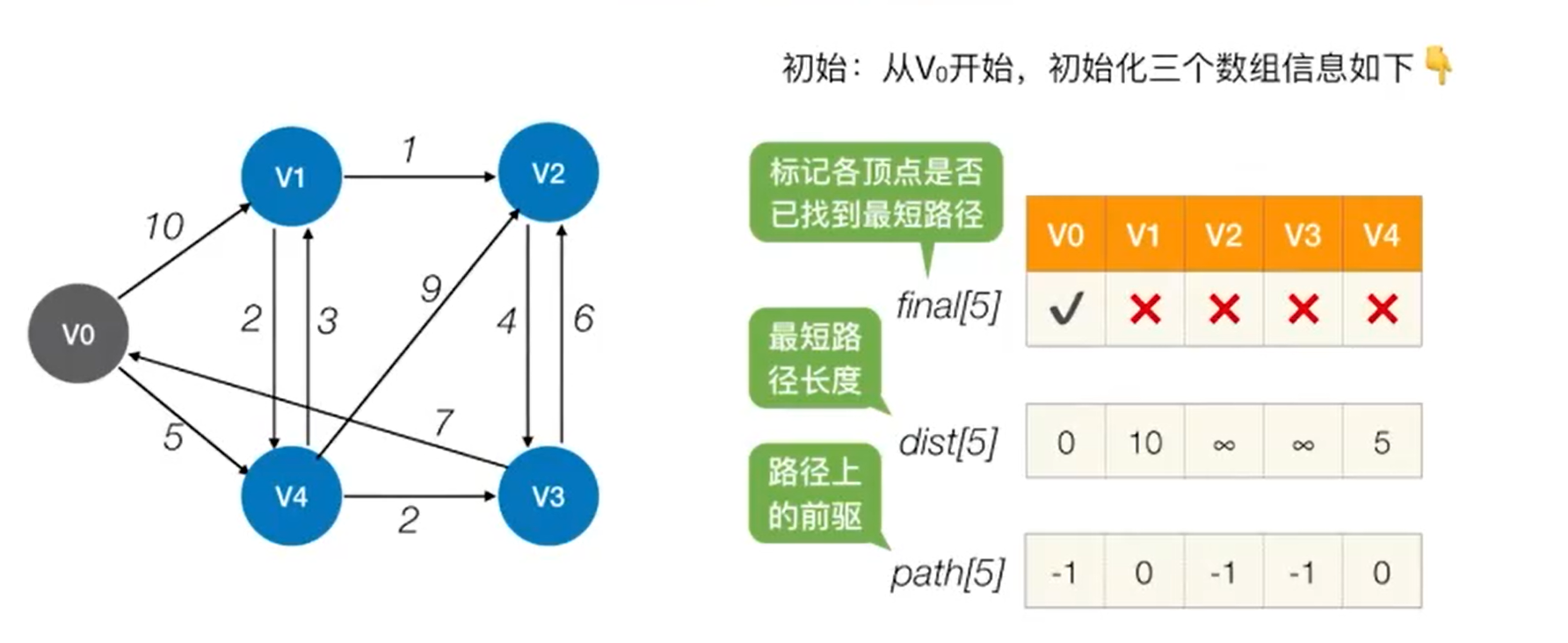
迪杰斯特拉 dijkstra

迪杰斯特拉最短路径主要解决单个结点到其他结点的最短路径问题。

简述过程如下：
1.循环记录最初结点能到达的结点的代价值到dist数组，此时假设最初节点到对应节点为最小代价，并将对应节点的前驱设置为最初结点，path[对应节点] = 最初结点
2.将最初结点标记为已完成，final[最初节点] = true
3.找到从当前能够到达的结点中最小代价的，且状态为未完成
4.将当前结点能达到的结点的代价值加上自己的代价值去对比当前的最小代价路线，如果 dist[当前结点] + 当前结点到目标结点的代价 < dist[目标节点] ， 那么则代表从当前结点到目标节点的代价是最小的，因此 dist[目标结点] = 当前结点到目标节点的代价，并替换前驱为当前结点
5.标记当前结点已完成

自此循环3、4、5直到全部结点都被标记已完成位置。此时便得到了从最初结点到所有结点的最小代价值，通过目标结点的前驱可以反推出最初结点到目标结点的最小代价路线。

弗洛伊德 floyd

弗洛伊德最短路径主要能够解决各项节点之间最短路径的问题。

1.初始化数组A，存储当前所有结点到目标节点的代价，path数组是存储当前结点最优路径的前驱，默认为无前驱(-1)
2.根据下列递推式进行计算，通过循环设立一个K为中转结点(0 ~ n)，结果是否优于当前结点直接到目标结点。
如果 Ai > Ai + Ak 成立，则代表通过K作为中转结点的代价会更小，因此将当前的最优代价替换为通过k中转后的结果，并在pathi 设为 k。

那么，最终的结果就是，每个结点到另外一个结点都是最优的，因为考虑到了所有结点可能的变化(循环使用 0 ~ n 的每个结点作为中转，并比较)。

拓扑排序

给定一个有向无环图，给出一个序列能够满足所有依赖项。

查找

二分查找

二分查找树

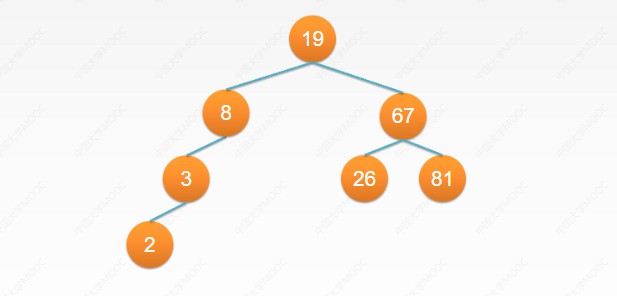
以左小右大的原则构成的一个二叉树，意味着左边的任意一个分支的值都比右边的任意一个都要大。其中特殊的一个性质是，对二叉查找树进行中序遍历的话，那么它就是一个有序队列。

平衡二叉查找树

如果将一个有序序列去做二叉树，那么带来查找目标值的时间复杂度退化为O(n)，变成了一个单链表。
而平衡二叉查找树的作用便是使一个二叉树尽量保持平衡性，即:每一个节点的左右子树的高度差<=1。 它的具体方法是如果插入的一个结点会导致树的不平衡，那么就通过旋转来调整平衡。

哈希表

哈希表就是建立元素值到某个字典key的映射，在此处我们理解为建立元素值到数组下标的映射。这样的话，我们可以直接通过数组随机访问的特性来直接判断该元素是否存在于我们的数据表之中。

在本书中，一般我们使用取余来为映射方法。即：f(x) = x%n; n为任意数字，因为此种方法过于简陋的缘故，必然会出现两个x得到的映射结果一样的情况，因此后面还由此引入了哈希冲突以及解决方法这个概念。

因此，我们通常对于映射方法f(x)中的n，设置为一个素数。

如: f(19) = 19 % 7 = 5，那么我们就将19这个数字放入下标为5的数组之中进行存放。

在理想情况下，即映射方法f(x)如果能使每一个x都分配到独一无二的下标之中，那么哈希表的查找效率是O(1).

哈希冲突解决办法

线性探测法

即在之前映射的基础上+1，继续使用哈希函数生成映射，直到一直循环到有一个数组位置是空的或者无位置为止。

链地址法

映射值如果是相同的话，那么就将对应的映射值组转换成一个链表结构。

排序

顾名思义，排序即为将一组无序的序列经过某个算法将其处理为有序序列。但不同的算法之间有着不同的区别。

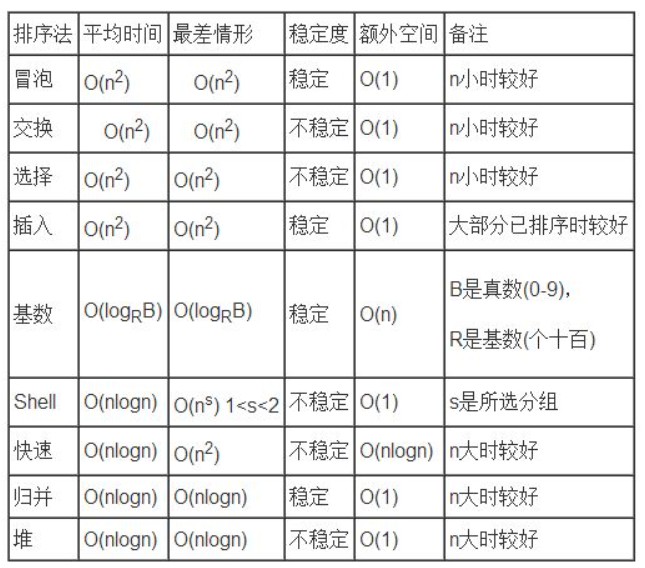
主要体现在以下三点。

  • 时间复杂度
  • 稳定性: 在序列之中相同的元素经过排序算法后不交换位置。在题目中相同的元素其中一个会加上下划线
  • 辅助空间: 即算法是否使用额外空间，其空间复杂度为多少

在考试之中一般以希尔排序、快速排序、堆排序为主，要求熟悉算法过程，而另外三个要求熟悉上述三个特点。

插入排序

选择排序

冒泡排序

归并排序

希尔排序(重点)

快速排序(重点)

堆排序(重点)

《数据结构与算法》学习笔记与一些代码题目的实现

https://ku-m.cn/index.php/archives/531/

作者

KuM

发布时间

2022-02-09

许可协议

CC BY 4.0

标签： 数据结构

本页的评论功能已关闭