LCS概述
LCS是一种使用动态规划解决两个字符串中共同的一组序列的最大值的一种方式。
LeetCode第1143题:longest-common-subsequence
首先我们需要知道什么叫做序列。
举例:A = 123 B = 342
那么它的子序列一共有:「3,2」。你可能会问‘32’应该也属于呀?这里需要说明,子序列可以隔一个数字,但不能更改其顺序,否则便成为子串,而不是子序列。
那么为什么要使用动态规划进行解决这个问题呢?前面我在再看深度优先算法中写了使用DFS获取所有子序列的方法,那么很简单,我们只需要求出所有子序列然后进行对比就可以了。不过这样的话时间复杂度就太高了,并不能这样进行编写。所以我们使用动态规划进行解决。
思路
主要的思路实际上就一句话: 逐个对比字符并且记录从前到后的数量。
主要递推式为: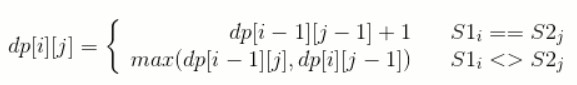
简单的概述,当 s[i-1] 与 s1[j-1]相等的时候,也就是发现一个共同序列的时候,那么dpi就等于在dpi-1的基础上+1。
反之,则取dpi-1与dpi的最大值。
代码
public static void main(String[] args) {
char[] s1 = "BSBININM".toCharArray();
char[] s2 = "JMJKBKJKV".toCharArray();
int[][] ans = new int[s1.length + 1][s2.length + 1];
for (int i = 1; i < s1.length + 1; i++) {
for (int j = 1; j < s2.length + 1; j++) {
if (s1[i - 1] == s2[j - 1]) {
ans[i][j] = ans[i - 1][j - 1] + 1;
} else {
ans[i][j] = Math.max(ans[i - 1][j], ans[i][j - 1]);
}
}
}
System.out.println(ans[s1.length][s2.length]);
for (int i = 1; i < ans.length; i++) {
for (int j = 1; j < ans[i].length; j++) {
System.out.print(ans[i][j] + " ");
}
System.out.println();
}
}
编辑距离
总的来说,目的是求出一个字符串到另外一个字符串所需的最少次数。
之前刷过一道这样的题目,记得是直接是使用BFS遍历各种可能,如果数据大肯定会超时2333。
LeetCode第72题:problems/edit-distance似乎是腾讯之前的面试题2333...
思路跟之前的一样,逐个对比。
String s1 = "horse";
String s2 = "ros";
首先我们知道,每一次对比,有两种可能: s1[i] 与 s2[j] 相同,和不相同。
假如二者相同,那么我们实际上只需要把上一次的结果拿过来就行了,即 dpi-1.
如果不相同呢?我们就需要考虑:替换、删除、添加,然后取其最小值。
例如我们的循环走到了 i = 1 , j = 1 。( 'h' 与 'r' 进行对比)。那么我们操作s1,删除就是i-1,即DPi-1。
而添加是DPi,替换是DPi-1。 这里好好思考一下为什么。
所谓我们的递推式就出来了。
(网上没找到图,直接上代码吧。)
if (s1.charAt(i-1) == s2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = 1 + Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]));
}
值得说明的是,我们需要考虑每一个字符串到空字符串的长度,即对应字符串的长度。
代码
String s1 = "abcde";
String s2 = "ad";
int[][] dp = new int[s1.length() + 1][s2.length() + 1];
for (int i = 0; i < s1.length()+1; i++) {
dp[i][0] = i;
}
for (int i = 0; i < s2.length()+1; i++) {
dp[0][i] = i;
}
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[i].length; j++) {
if (s1.charAt(i-1) == s2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = 1 + Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]));
}
}
}
System.out.println(dp[s1.length()][s2.length()]);