前言

这几天刷了很多道搜索的算法题，回头又看之前发的相关博文，简直解释的一蹋糊涂，我承认当时并没有完全掌握，东扯西扯哈哈哈。
其实深度优先算法（DFS）是一种思想，相对于广度优先搜索（BFS)而言，它的表现是，先进入最深层对象，然后回溯上来。脱离回溯这个词，实际上它与递归并没有什么区别，也就是更高级一些的暴力算法。所以没有必要把它想的太过于复杂，只是有一些抽象，有些难理解，在纸上推导几遍就清楚了。

概述

现有楼梯十层，小明可以走一步或两步，那么当走到第十层的时候一共有多少中走法？
这一题很简单，我们只需要在第一层的时候考虑，我有几种方法。很容易想到，两种，要么走一步，要么走两步，那我们就写两个递归就行了。出口是第十层，并且过滤掉大于10层的。

    public static void f(int step){
    if (step > 10) return;
    if (step == 10) {
        ans++;
    }
    f(step+1);
    f(step+2);
    
}

仔细思考，其实像这种递归也就是先进入更深层次，然后再慢慢的递归回来。那什么是DFS呢？回溯又是什么呢？
我们先更改一下上面的题目。

现有楼梯十层，小明可以走一步或两步，现在要求你输出这一路线过程，如： 1>2>3>4>5>6>7>8>9>10

如何编写？实际上我们可以通过函数参数的传递进行记录他的路线，但我要叙述的是DFS，先过滤掉这个想法。
先贴上解决这个问题的代码：

    public static void f(int step,List<Integer> l){
    if (step>10) return;
    if (step == 10) {
        for (int i = 0; i < l.size(); i++) {
            System.out.print(l.get(i) + "=>");
        }
        System.out.print("10");
        System.out.println();
    }else {
        l.add(step);
        f(step+1,l);
        f(step+2,l);
        l.remove(l.size()-1);
    }
    
}

我们没有走到目标楼层的情况下，对当前的list参数加入当前的层数，然后达到记录的目的。然后在当前层数中执行下一层的两种走法的函数。这点估计都能理解，那么为什么要最后删除list中最后一个元素呢？ 可以着手测试，如果没有最后一句命令，到目标值的时候必然是一大段无意义的答案。

而使用这条命令呢？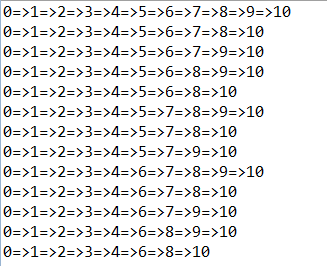

这些便是正确答案。为什么？ 如果不仔细思考，你肯定完全蒙圈了。我们这个时候画图分析一下。

如图所示，这便是回溯。相同的还可以使用这种思想解决数字全部排列问题（DFS排列）。最大的建议就是，用一张纸进行推到几遍，就明白了~

DFS排列数字

import java.util.ArrayList;

class Main {

static int[] vis = new int[9];

public static void main(String[] args) {

    f(0, new ArrayList<Integer>());

}

private static void f(int step, ArrayList<Integer> l) {
    // TODO Auto-generated method stub

    if (step == 9) {
        for (int i = 0; i < l.size(); i++) {
            System.out.print(l.get(i));
        }
        System.out.println();

    } else {

        for (int i = 0; i < 9; i++) {
            if (vis[i] == 0) {
                vis[i] = 1;
                l.add(i + 1);
                f(step + 1, l);
                vis[i] = 0;
                l.remove(l.size() - 1);
            }

        }

    }

}

}

DFS求集合所有子集

假设每一位数字有两种状态，一种是存在，一种是不存在。那么我们在递归的时候就可以求出所有的子集。

import java.util.*;

class Main{
    static int[] arr = {3, 4, 1, 2};
    public static void main(String[] args) {
        boolean[] vis = new boolean[4];
        f(0,vis);
    }

    static void f(int step, boolean[] vis) {
        if (step == arr.length) {
            List<Integer> list = new ArrayList<>();
            for (int i = 0; i < arr.length; i++) {
                if (vis[i]){
                    list.add(arr[i]);
                }
            }
            System.out.println(list);

        } else {
            vis[step] = false;
            f(step+1,vis);
            vis[step] = true;
            f(step+1,vis);
        }
    }

DFS求所有子序列

   public static void f(int index, List<Integer> list) {
        if (index > arr.length) {
            System.out.println(list);
        } else {
            for (int i = index; i <= arr.length; i++) {
                int temp = -1;
                if (i < arr.length) {
                    temp = arr[i];
                }
                list.add(temp);
                f(i + 1, list);
                list.remove(list.size() - 1);
            }

        }
    }
}